原理
将问题分解为几个规模较小但类似于原问题的子问题,递归求解这些子问题,然后合并这些子问题的解来建立原问题的解
分治模式在每层递归时,都有三个步骤:
1. 分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。2. 解决这些子问题,递归地求解各个子问题。如果子问题规模足够小,直接求解3. 合并子问题的解为原问题的解归并排序
以归并排序为例,归并排序的操作如下:
分解:分解待排序的n个元素的序列为具有n/2个元素的两个子序列解决:使用归并排序递归地排序两个子序列合并:合并两个已排序的子序列以产生已排序的答案当待排序的序列长度为1时,递归开始回升,在这种情况下不要做任何工作,因为长度为1的序列已排序好了void mergeArr(int* arr, int startIdx, int mid, int endIdx){ int n1 = mid - startIdx; int n2 = endIdx - mid; // 用两个临时数组,保存要合并数组的值 int* a1 = new int[n1]; int* a2 = new int[n2]; for (int i = 0; i < n1; i++) { a1[i] = arr[startIdx+i]; } for (int i = 0; i < n2; i++) { a2[i] = arr[mid+i]; } // 按照从小到大的顺序,合并两个数组的值 int len = n1 + n2; int i = 0, j = 0; for (int k = startIdx; k < endIdx; k++) { if (j == n2) { arr[k] = a1[i++]; } else if (i == n1 || a1[i] > a2[j]) { arr[k] = a2[j++]; } else { arr[k] = a1[i++]; } } delete[] a1; delete[] a2;}// arr表示待排序的数组,startIdx,endIdx分别表示数组中元素的索引,前闭后开区间void merge_sort(int* arr, int startIdx, int endIdx){ if (endIdx - startIdx == 1) { return; } // 分解 int mid = (startIdx+endIdx) >> 1; merge_sort(arr, startIdx, mid); merge_sort(arr, mid, endIdx); // 合并 mergeArr(arr, startIdx, mid, endIdx);}
最大子数组问题
以茅台股票的股价走势日线图为例,如下图。假如我们能够穿越时空,回到过去,给你足够买一手茅台的钱,只买卖一次,你怎样可以实现最大化收益。
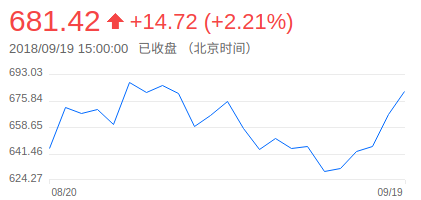
茅台一个月的收盘价:[644.79, 671.49, 667.7, 670.21, 660.3, 687.3, 681.0, 685.85, 680.4, 659.19, 666.21, 675.04, 657.79, 644.0, 650.97, 644.8, 646.0, 630.0, 631.98, 642.9, 645.81, 666.7, 681.42]
一种方法是暴力求解:尝试每对可能的买进和卖出组合,只要卖出日期在买入日期之后即可。n天时间的组合有 n+n-1+n-2+...+1 = O(n^2) 种。
下面使用分治法来求解。
首先变化一下思路,我们将股价每天的变化值列出来,得到一个新的数组:
[26.7, -3.79, 2.51, -9.91, 27.0, -6.3, 4.85, -5.45, -21.21, 7.02, 8.83, -17.25, -13.79, 6.97, -6.17, 1.2, -16.0, 1.98, 10.92, 2.91, 20.89, 14.72]
这样我们原来的问题就转化成:寻找A中最大的非空连续子数组。
分治法三步骤:分解,解决,合并
先把数组分解,假定我们寻找子数组A[low...high]的最大子数组。我们可以找到子数组中央位置mid,然后求解两个子数组A[low...mid]和A[mid+1...high]
A[low...high]的任何连续子数组A[i...j]所处位置有三种情况:
1. 完全位于A[low...mid]中, low <= i <= j <= mid
2. 完全位于A[mid+1...high]中, mid < i <= j <= high
3. 跨越了中点,low <= i <= mid < j <= high
1和2两种情况是原问题的子问题,第3中情况,可以由两个子数组 A[i...mid] 和 A[mid+1...j] 组成。我们只需要找出形如 A[i...mid] 和 A[mid+1...j] 的最大子数组,然后合并就可以了。
#include#include #include double cross_subarray(double* arr, int low, int mid, int high, int& left, int& right){ // 左边的最大子数组,arr[mid]肯定被选中 double leftsum = arr[mid] - 1; double sum = 0; for (int i = mid; i >= low; i--) { sum += arr[i]; if (sum > leftsum) { leftsum = sum; left = i; } } // 右边的最大子数组,arr[mid]肯定被选中 double rightsum = arr[mid] - 1; sum = 0; for (int i = mid; i <= high; i++) { sum += arr[i]; if (sum > rightsum) { rightsum = sum; right = i; } } // arr[mid]被计算了两次,减去一次 return leftsum + rightsum - arr[mid];}double max_sub_array(double* arr, int low, int high, int& left, int& right){ if (low == high) { left = right = low; return arr[low]; } else { int mid = (low + high) >> 1; int left_low, left_high, right_low, right_high, cross_low, cross_high; double left_sum = max_sub_array(arr, low, mid, left_low, left_high); double right_sum = max_sub_array(arr, mid+1, high, right_low, right_high); double cross_sum = cross_subarray(arr, low, mid, high, cross_low, cross_high); if (left_sum >= right_sum && left_sum >= cross_sum) { left = left_low; right = left_high; return left_sum; } else if (right_sum >= left_sum && right_sum >= cross_sum) { left = right_low; right = right_high; return right_sum; } else { left = cross_low; right = cross_high; return cross_sum; } }}int main(){ double arr[] = { 26.7, -3.79, 2.51, -9.91, 27.0, -6.3, 4.85, -5.45, -21.21, 7.02, 8.83, -17.25, -13.79, 6.97, -6.17, 1.2, -16.0, 1.98, 10.92, 2.91, 20.89, 14.72}; int len = sizeof(arr) / sizeof(double); int left, right; double sum = max_sub_array(arr, 0, len-1, left, right); printf("%d, %d, %lf\n", left, right, sum); for (int i = left; i <= right; ++i) { printf("%lf ", arr[i]); } printf("\n"); return 0;}
打印结果:
17, 21, 51.420000 1.980000 10.920000 2.910000 20.890000 14.720000
如果能往前回几天,可以在9.13号买,今天卖的话,一股赚51.42,一手赚5142
如果能往前回几年,那就无脑买吧,因为茅台的股价走势是这样的:

哈哈,我真能幻想